Crystallography Basics
Basics of Crystallography
Q1. What is a crystal?
Q2. What is a crystal structure?
Q3. What is a unit cell and lattice?
Q4. How does the arrangement of atoms help determine the crystal structure?
A1. A crystal consists of matter that is formed of an ordered three dimensional arrangement of atoms, molecules or ions. This can be imagined as the stacking of bricks in a wall (resembling to a two dimensional ordered arrangement of bricks!).
| 2D Ordered Arrangement of Bricks | 3D Ordered Arrangement of atoms |
 |  |
Q2. What is a Crystal Structure?
A2. A crystal structure is a unique arrangement of atoms, molecules or ions in a crystal. It is composed of a motif, which is a set of atoms arranged in a particular way, and a lattice. Motifs are located upon the points of lattice, which is an array of points repeating periodically in three dimensions. The points can be thought of as forming identical tiny boxes, called unit cells, that fill the space of lattice.
The lengths of the edges of a unit cell and the angles between them are called the lattice parameters.
It is often observed in the nature that one element/ molecule can exist in different crystal structure based on the differences in the periodic arrangement of atoms with respect to each-other. This property of materials to be able to exist in more than one form or crystal structure is called the polymorphism.
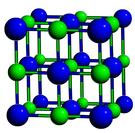
An example of polymorphism that is easily seen in our daily lives is Carbon; it exists as Diamond and Graphite of which diamond is the hardest material which is used in cutting tools and also jewellery. However, graphite is a soft material, which finds use in our pencils, and lubrication. The figures below shows the fundamental differences of how the atoms are arranged in a three dimensional arrays in diamond and graphite which are both composed of the same element carbon.
| Carbon atoms in diamond | Carbon atoms in graphite |
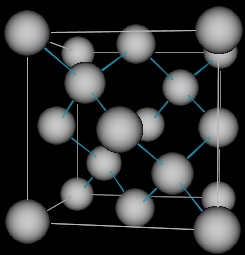 | 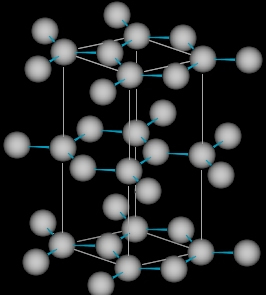 |
Q3. What is a unit-cell and lattice? Is there any classification of unit-cell and lattices based on the atomic arrangment?
A3. A unit-cell is the smallest building block of a crystal and is representative unit of the repetative motifs in the crystal structure.
Lattice is the geometrical basis of all the crystals. A lattice can be considered as a regular and infinite arrangement of points/ atoms where in each point/ atom has the same surrounding environment. This is equally applicable in one, two and three dimensional space.
Lattices in a three dimension have three non co-planar lattice constants (like a shoe-box!) indicated by the translation vectors a, b, & c(sometime referred as x, y, and z respectively for three vertices facing perpendicular to each-other), and angle between the three vertices bc, ac, and ab indicated by α (alpha), β (beta), and g (gamma) respectively.
Let us begin with two dimensional lattice which, can be considered as a net as shown below.
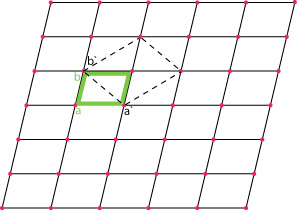
The net lattice is the array of points (shown as pink dots!). This net lattice (above) represents a twofold rotational symmetry about each pink point (representing the position of atom).
To chose the unit-cell a universal crystallographic convention is followed; the unit cell is the smallest repeat unit for which its delineating vectors are parallel to, or coincide with, important symmetry directions in the lattice. In the figure above a and b is a possible unit cell, but it does not give information about lattice symmetry if seen in isolation. However, a` and b`(in green) coincide with the symmetry lines (mirror) in the net so it is preferred.
Three dimensional lattices, (also known as Bravais Lattices) can be imagined as being developed by the regular stacking of nets. There are 14 ways in which this can be done as shown below:
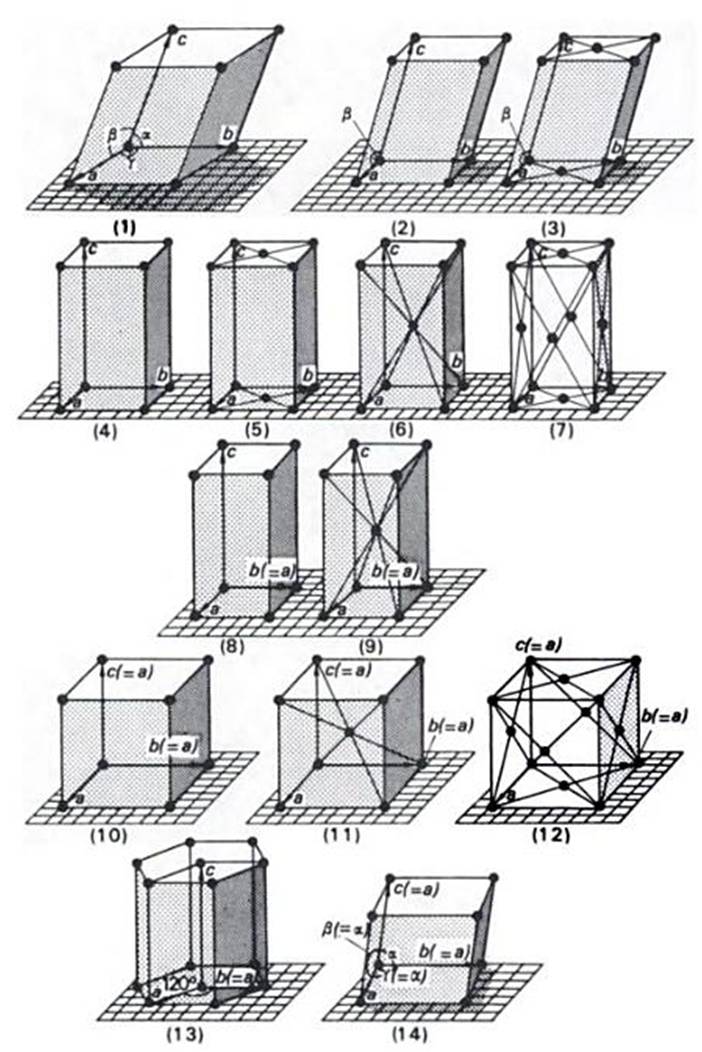
Each lattice is represented by a unit-cell, outlined by three vectors a, b, and c. In accordance with convention, these vectors are chosen so that they both form a parallelpipedon of smallest volume in the lattice and are parallel to, or coincide with, important symmetry directions in the lattice, so that not all conventional unit cells are primitiive. In three dimensions, we encounter unit cells centered on a pair of opposite faces, body-centered, or centered on all faces.
For more information read the book mentioned in the reference.
Reference: Structure Determination by X-ray Crystallography, M.F.C. Ladd & R.A. Palmer, 3rd Edition, Plenum Press, NY.
Q4. How do the different arrangement of atoms in a unit-cell and lattice help in determining the crystal structure of a compound?
A4. Due to the different arrangement of atoms in a unit-cell, X-rays are diffracted in different patterns. Each structure has a unique X-ray diffraction pattern (comparable to human finger prints) that gives the information about the definite spatial arrangement of atoms in a unit-cell and lattice. This, in turn, gives the information about the crystal structure.